变分自编码器（Variational Autoencoders，VAE）详解：数学原理、图示、代码

本文首先介绍 VAE 中用到的基本统计学知识，然后简要介绍 VAE 的核心点（贡献），继续通过代码示例，了解 VAE 的整个架构。对 VAE 的原理有兴趣的，可以看后面的概率论原理部分。

本文内容

前置知识
VAE 主要技术点
代码示例
VAE（变分自编码器）的概率论原理
VAE 中的概率模型选择
应用
参考资料

前置知识

统计学中相关术语

概率密度函数（Probability Density Function，PDF）描述连续型随机变量的概率分布情况的函数，它表示随机变量在某个特定值附近的概率密度，表示如 $p(x)$ 。概率质量函数（Probability Mass Function，PMF）则描述离散型随机变量的概率分布情况的函数，它表示随机变量取某个特定值的概率。

累积分布函数（Cumulative Distribution Function, CDF）是 PDF 的积分形式。对于一个随机变量 $X$ ，它的累积分布函数 $F(x)$ 定义为 $F(x) = P(X ≤ x)$ ，即随机变量 $X$ 取值小于或等于 $x$ 的概率。

分布参数（Distributional Parameters）：描述概率分布的特征或性质的数值。这些参数定义了分布的具体形状和行为。例如，在正态分布（也称为高斯分布）中，分布的参数包括均值 μ（Mean）和标准差 σ（Standard Deviation），VAE 算法中，Encoder 神经网络的输出即这两个参数。分布参数通常表示为 $\theta,\phi$ ，在密码函数中的示例如 $p_{\theta}(x)$ 。

先验分布（prior distribution）是指在进行统计试验或随机抽样之前，根据已有的知识或经验对某一未知参数 $θ$ 或随机变量所做出的概率分布估计。例如，后面假定隐变量 $z$ 的分布为标准正态分布。

后验分布（Posterior Distribution）是贝叶斯统计中的一个核心概念，它指的是在观测到数据之后，对参数 $θ$ 或潜变量的分布的更新。

独立同分布（independently and identically distributed，缩写 i.i.d.）

边际分布（Marginal Distribution）是概率论和统计学中的一个概念，具体指在多维随机变量中，只包含其中部分变量的概率分布。换句话说，当我们关注多维随机变量中的某一特定变量时，可以通过边际分布来得到这个变量的概率分布，而不必考虑其他变量的影响。这实际上是一个降维操作。

例如，假设有两个变量相关的概率分布P(x,y)，关于其中一个特定变量（如x）的边缘分布则为给定另一个变量（如y）的条件概率分布。这样，我们可以只关注变量x的概率分布，而不再考虑变量y的影响。
在实际应用中，比如在人工神经网络中，由于神经元之间互相关联，计算它们各自的参数时，就会使用边缘分布来得到某一特定神经元（变量）的值。

生成和推理

推理（Inference）和生成（Generation）是人工智能和机器学习中的两个关键概念，这两个词在论文中经常出现（如后面会聊到的 Variational Inference），这里简要说明一下。

推理是指使用已训练的模型对新的、未见过的数据进行预测或推导。它是将模型在训练过程中学到的知识应用于具体任务的过程。

生成是指根据模型学到的模式创建新的数据或内容。它涉及生成新的输出，通常是模仿或基于训练数据。

方面	推理	生成
目的	预测结果（如分类、回归）。提取信息（如情感分析、目标检测、获取 Embedding）。	根据学到的模式创建新数据（如文本、图像、音乐）。
输入	用于评估或使用的真实世界数据。	一个提示或种子（如起始文本、一个主题）。
输出	预测的标签、数值或决策。	新的、合成的数据（文本、图像等）。
示例	给定一张图片，判断是否包含一只猫（分类）。根据历史天气数据预测明天的气温。	根据一个主题生成一段文字（语言模型）。根据描述创建一张图片（如 DALL·E）。
复杂性	使用模型训练时学到的固定参数，通常速度快，适合实时应用。	生成涉及从模型的概率分布中进行采样。可能需要创意或随机性以产生多样化的输出。
结果	模型对数据进行解释，但不会生成新数据。	创造新的内容。

潜变量

潜在变量（又称隐变量）是统计学、机器学习中的一个重要概念。与可以直接测量或观察的可观测变量不同，潜在变量代表那些不能直接观察但可以从其他可测量变量中推断出来的潜在因素。

引入潜变量后，在概率背景下，推理和生成可以如下描述。

为了推理（推断）潜在变量，我们给定或者从数据集（即 $p(x)$ ）中抽样 $x$ ，然后根据 $p(z{\mid}x)$ 中采样 $z$ 。

x \sim p(x)

z \sim p(z|x)

为了生成一个数据点，我们根据潜变量的概率分布 $p(z)$ ，采样出 $z$ ，然后根据 $p(x{\mid}z)$ 再采样数据点 $x$ 。

z \sim p(z)

x \sim p(x|z)

为什么要引入潜变量呢？先看一个具体的例子。

如图 1， $x$ 变量的分布不容易简单描述。 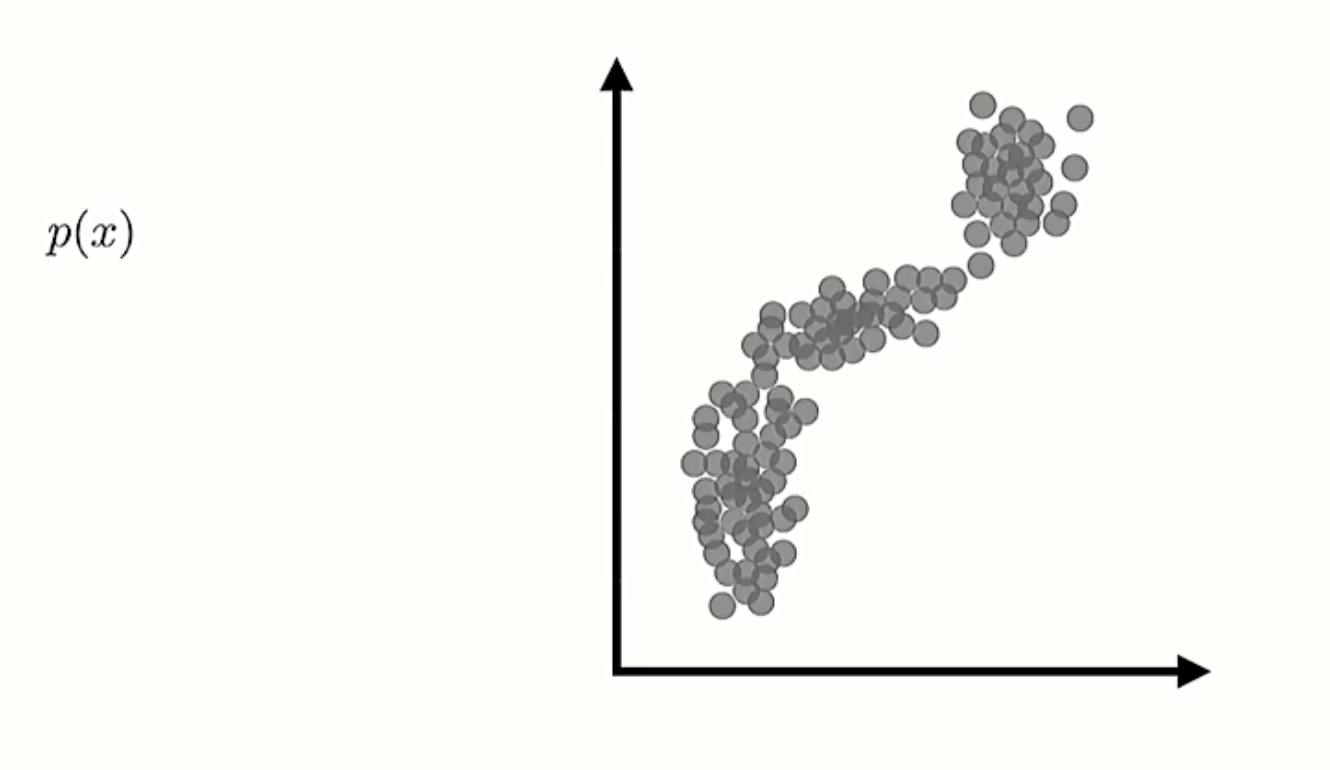图 1： $x$ 的分布，图片来源 Stanford CS330 课程

如图 2，引入潜变量 $z$ ，描述 $x$ 变量的分布变得简单。其中 $z$ 有三个取值，给定 $z$ 后， $p(x \mid z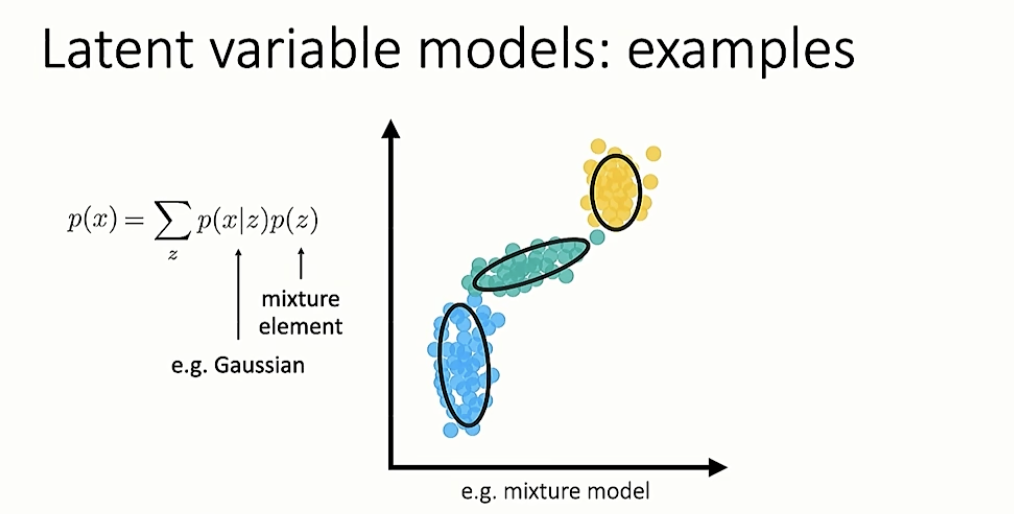)$ 类似一个高斯分布。 图 2： $X$ 的分布，图片来源 Stanford CS330 课程

推广到一般的情况。图 3 是一般的基于高斯分布的潜变量模型。 $x$ 的密度函数 $p(x)$ 非常复杂，但是，可以通过如下方式描述：
（1）引入潜变量 $z$ （来自高斯分布，相对简单）
（2）引入条件概率密度函数 $p(x|z)$ ，也是高斯分布（相对简单）
（3）针对每 1 个取定的 $z$ 值，对应一个 $x$ 的密度函数，其可以用神经网络输出均值 $u$ 和方差 $σ$ 的方式描述。
这里要注意， $z$ ， $x$ 都可能是多个维度的，每个维度之间不是独立的，所以该神经网络相对复杂。

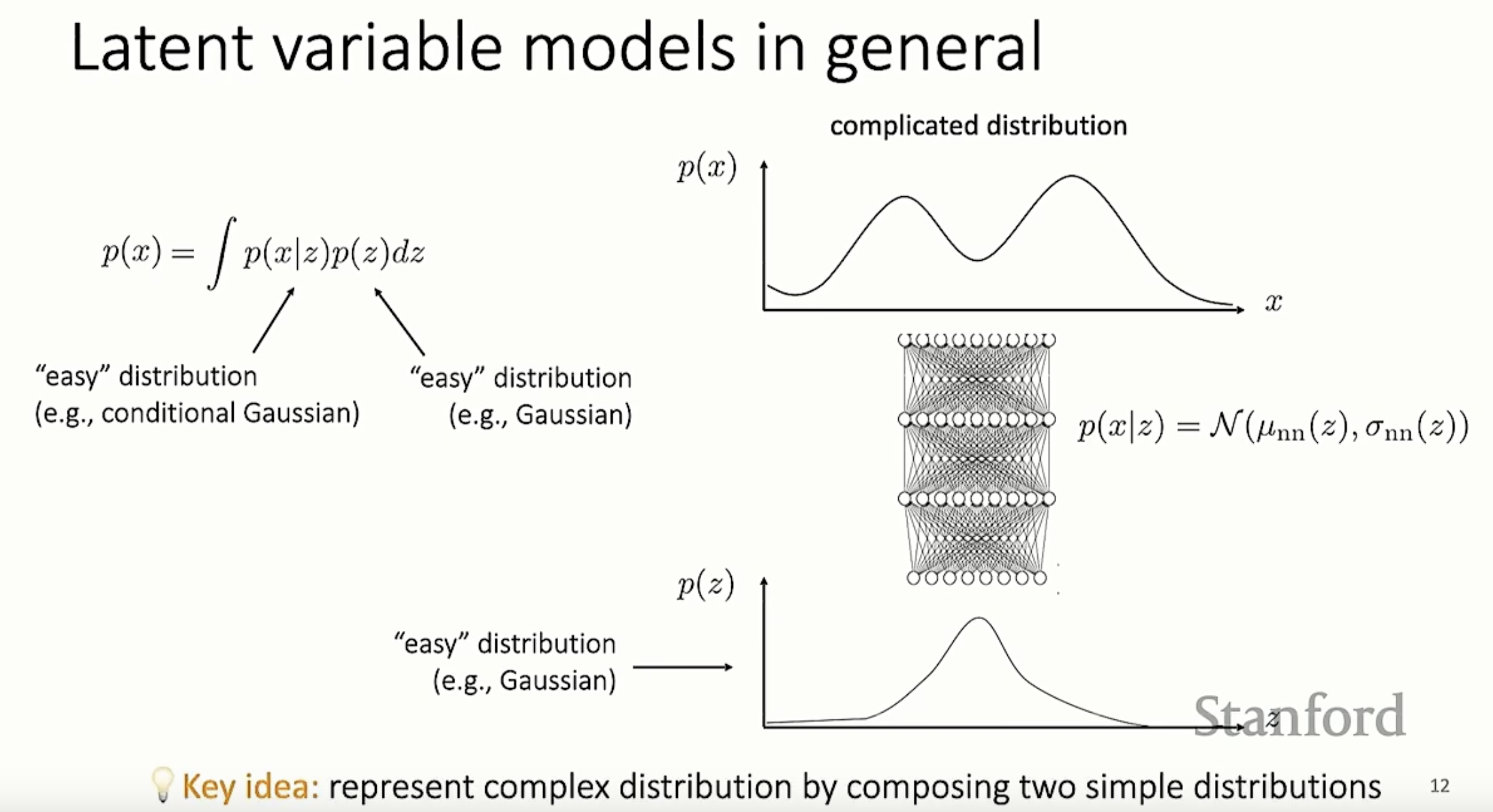图 3：一般的潜变量模型，图片来源 Stanford CS330 课程

图 4 来自李宏毅教授的讲义，概念类似图 3。 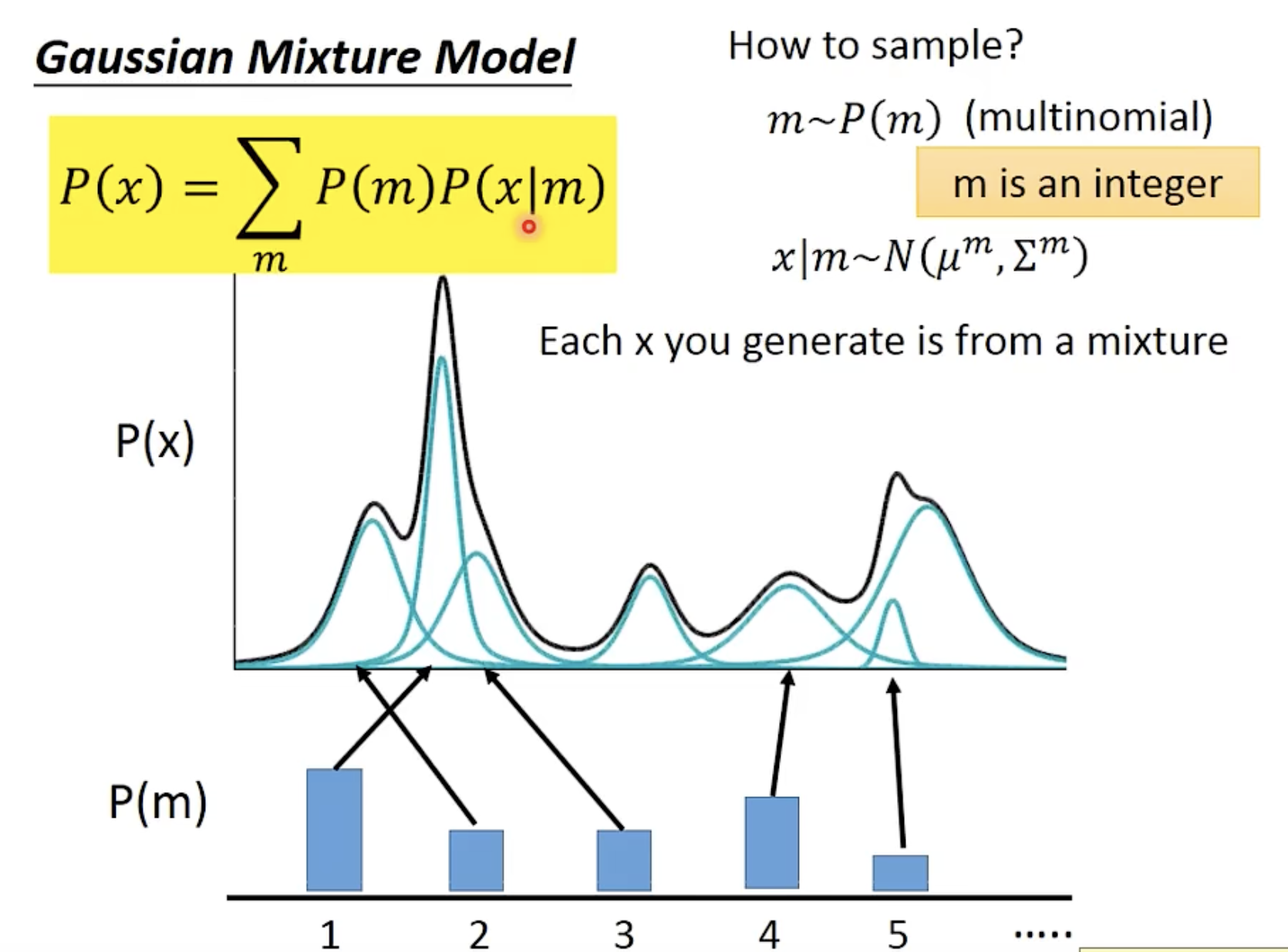图 4：隐变量模型示意图，李宏毅教授的讲义

贝叶斯定理（基于潜在变量）

假设我们有观测数据 $x$ 和潜在变量 $z$ ，我们希望通过贝叶斯推断得到后验分布 $p(z{\mid}x)$ ，即在给定观测数据 $x$ 的情况下，潜在变量 $z$ 的分布。

贝叶斯定理用于建立这一后验分布：

p(z|x) = \frac{p(x|z)p(z)}{p(x)}

其中：

$p(z{\mid}x)$ ：后验分布，表示我们在观察到数据 $x$ 后对潜在变量 $z$ 的信念更新。
$p(x{\mid}z)$ ：似然函数，表示在潜在变量 $z$ 给定的情况下，数据 $x$ 出现的可能性。
$p(z)$ ：先验分布，表示我们对潜在变量 $z$ 的先验知识。
$p(x)$ ：边缘似然，作为标准化因子，确保后验分布的总概率为 1。

VAE 主要技术点

摊销变分推理（Amortized Variational Inference）

摊销变分推理（Amortized Variational Inference）是一种在变分自编码器（VAEs）的技术。在这种方法中，变分参数（即用于近似后验分布的参数）不是针对每个数据点单独优化的，而是跨数据点共享的，并通过一个神经网络（通常是编码器网络）进行参数化。

变分自编码器

变分自编码器（VAEs）属于变分贝叶斯方法的一族。尽管变分自编码器与基本自编码器在架构上相似，但它们具有不同的目标和完全不同的数学公式。VAE 中的潜在空间（latent space）是由一系列分布（distributions）组合而成，而不是一个固定的向量。

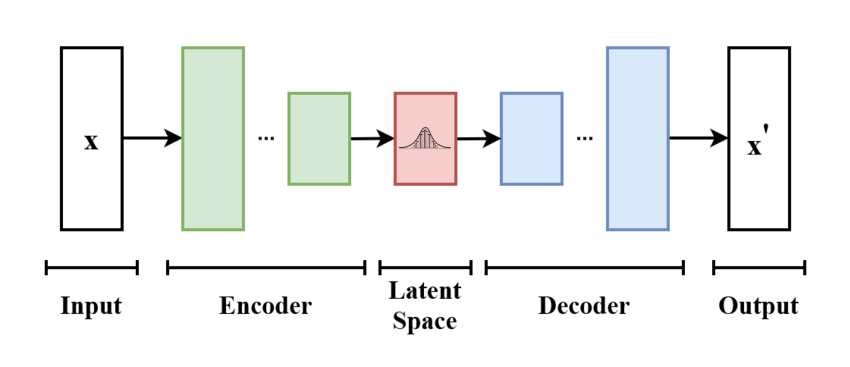变分自编码器的基本方案如下：模型接收 $x$ 作为输入。编码器将其压缩到潜在空间。解码器接收从潜在空间采样的信息作为输入，并生成尽可能与 $x$ 相似的 $x'$ 。

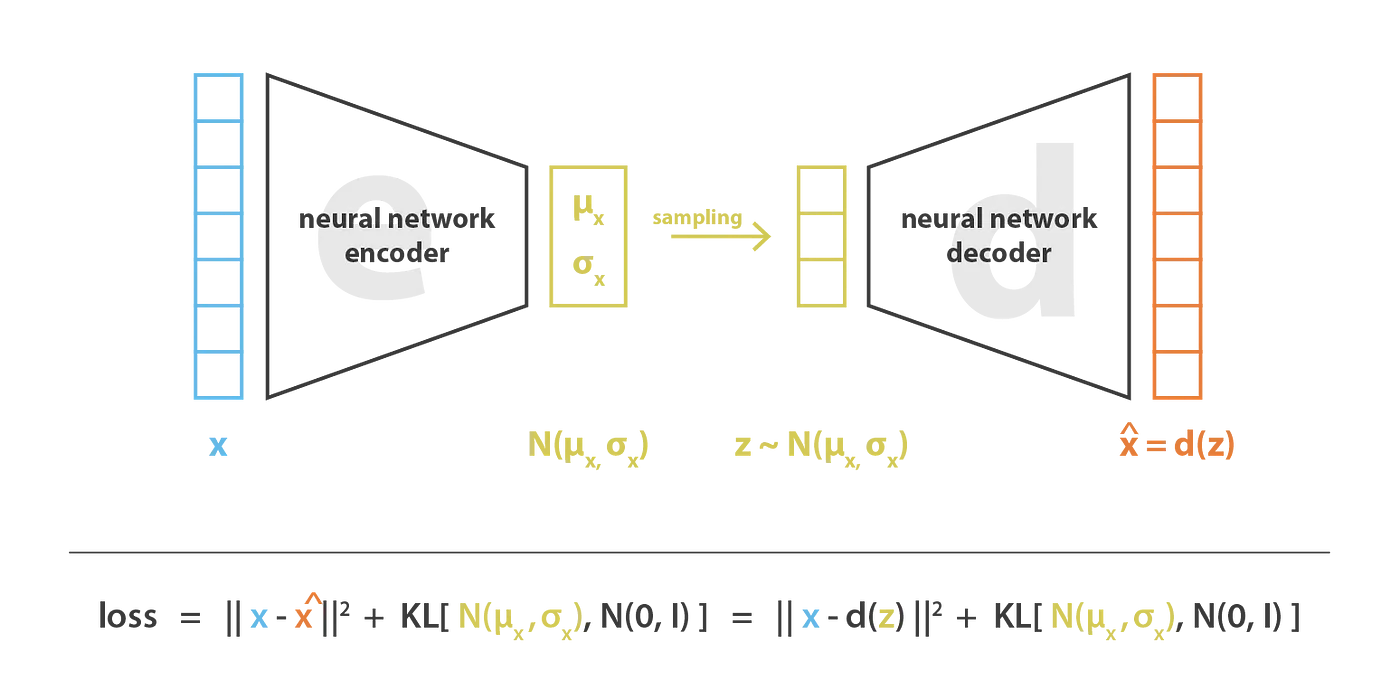变分自编码器中，损失函数由重构（reconstruction）项（使编码解码方案高效）和正则化项（使潜在空间表示符合正态分布）组成。

这里涉及到一个机器学习的梯度下降问题。注意，Encoder 网络输出的是潜变量 z 这个随机变量的均值和方差。需要经过抽样，才能产生有具体数值的 z 值，然后通过 decoder 网络生成 x。抽样这一步无法做梯度下降，为了解决这个问题，VAE 作者提出了“重参数化技巧”的解决思路。

梯度下降问题的解决思路：重参数化技巧

根据 VAE 论文作者的说法，变分自编码器（VAE）框架的最大贡献可能就是“重参数化技巧”。

Perhaps the greatest contribution of the VAE framework is the realization that we can counteract this variance by using what is now known as the “reparameterization trick”, a simple procedure to reorganize our gradient computation that reduces variance in the gradients. （来源：arXiv:1906.02691）

变分参数 $φ$ 通过随机变量 $z \sim q_\phi(z \mid x)$ 影响目标函数 $f$ 。

假如用 SGD 的方法，通过计算梯度 $∇_φf$ 来优化目标函数，基于原来的形式（图 7 左，如下公式），我们无法对 $f$ 关于 $φ$ 求导，因为无法通过随机变量 $z$ 直接反向传播梯度。

\mathbf{z} \sim q_\phi(\mathbf{z}\vert\mathbf{x}^{(i)}) = \mathcal{N}(\mathbf{z}; \boldsymbol{\mu}^{(i)}, \boldsymbol{\sigma}^{2(i)}\boldsymbol{I})

作者通过将变量 $z$ 重新参数化为 $φ$ （确定性且可微分）、 $x$ 和新引入的随机变量 $\epsilon$ ，来“外部化” $z$ 中的随机性，进而能够通过 $z$ 进行反向传播，并计算梯度 $∇_φf$ （图 7 右，如下公式）。也就是说，从最终 $f$ 的输出到 $φ$ 参数的反向传播路径上，不再有随机变量的抽样了。从后面的代码示例（ epsilon = tf.random.normal(shape=(batch, dim)) 和 return z_mean + tf.exp(0.5 * z_log_var) * epsilon ）也可以看出。

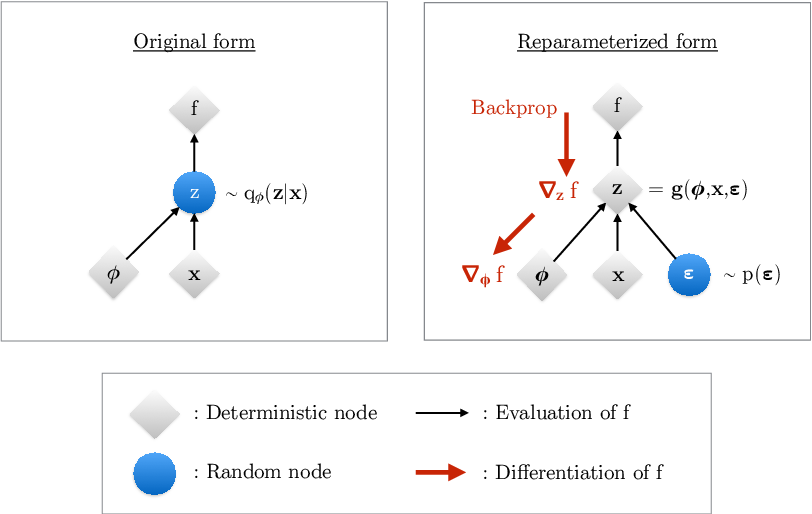\mathbf{z} = \boldsymbol{\mu} + \boldsymbol{\sigma} \odot \boldsymbol{\epsilon} \text{, where } \boldsymbol{\epsilon} \sim \mathcal{N}(0, \boldsymbol{I})

图7：重参数化技巧（reparameterization trick）的说明。（来源于论文 arXiv:1906.02691）

代码示例

# 参考：https://keras.io/examples/generative/vae/
import os
os.environ["KERAS_BACKEND"] = "tensorflow"
import numpy as np
import tensorflow as tf
import keras
from keras import layers

# 抽样
class Sampling(layers.Layer):
    """Uses (z_mean, z_log_var) to sample z, the vector encoding a digit."""

    def call(self, inputs):
        z_mean, z_log_var = inputs
        batch = tf.shape(z_mean)[0]
        dim = tf.shape(z_mean)[1]
        # 从正态分布中随机抽样。
        # 这个实现方式和论文中的重参数化技巧（reparameterization trick）对应。
        epsilon = tf.random.normal(shape=(batch, dim))
        return z_mean + tf.exp(0.5 * z_log_var) * epsilon

## ---------- encoder ----------
latent_dim = 2 # 隐含层表示的向量维度为 2，即均值、方差都是用两个浮点数表示。
encoder_inputs = keras.Input(shape=(28, 28, 1))
x = layers.Conv2D(32, 3, activation="relu", strides=2, padding="same")(encoder_inputs)
x = layers.Conv2D(64, 3, activation="relu", strides=2, padding="same")(x)
x = layers.Flatten()(x)
x = layers.Dense(16, activation="relu")(x)
z_mean = layers.Dense(latent_dim, name="z_mean")(x)
# 训练后的方差。
z_log_var = layers.Dense(latent_dim, name="z_log_var")(x)
# 根据均值和方差（取 log 后）抽样
z = Sampling()([z_mean, z_log_var])
encoder = keras.Model(encoder_inputs, [z_mean, z_log_var, z], name="encoder")
encoder.summary()

## ---------- decoder ----------
latent_inputs = keras.Input(shape=(latent_dim,))
x = layers.Dense(7 * 7 * 64, activation="relu")(latent_inputs)
x = layers.Reshape((7, 7, 64))(x)
x = layers.Conv2DTranspose(64, 3, activation="relu", strides=2, padding="same")(x)
x = layers.Conv2DTranspose(32, 3, activation="relu", strides=2, padding="same")(x)
decoder_outputs = layers.Conv2DTranspose(1, 3, activation="sigmoid", padding="same")(x)
decoder = keras.Model(latent_inputs, decoder_outputs, name="decoder")
decoder.summary()

# ---------- 用于训练的模型 ----------
class VAE(keras.Model):
    def __init__(self, encoder, decoder, **kwargs):
        super().__init__(**kwargs)
        self.encoder = encoder
        self.decoder = decoder
        self.total_loss_tracker = keras.metrics.Mean(name="total_loss")
        self.reconstruction_loss_tracker = keras.metrics.Mean(name="reconstruction_loss")
        self.kl_loss_tracker = keras.metrics.Mean(name="kl_loss")

    @property
    def metrics(self):
        return [
            self.total_loss_tracker,
            self.reconstruction_loss_tracker,
            self.kl_loss_tracker,
        ]

    def train_step(self, data):
        with tf.GradientTape() as tape:
            z_mean, z_log_var, z = self.encoder(data)
            # z 是基于均值和方差抽样的，不是直接计算的数据。
            reconstruction = self.decoder(z)
            # 用交叉熵衡量生成的图和原图的差异。
            reconstruction_loss = tf.reduce_mean(
                tf.reduce_sum(
                    keras.losses.binary_crossentropy(data, reconstruction),
                    axis=(1, 2),
                )
            )
            # 计算 kl_loss，推导方法请参考后面的公式（6.1）
            kl_loss = -0.5 * (1 + z_log_var - tf.square(z_mean) - tf.exp(z_log_var))
            kl_loss = tf.reduce_mean(tf.reduce_sum(kl_loss, axis=1))
            # 总损失是两者之和
            total_loss = reconstruction_loss + kl_loss
        grads = tape.gradient(total_loss, self.trainable_weights)
        self.optimizer.apply_gradients(zip(grads, self.trainable_weights))
        self.total_loss_tracker.update_state(total_loss)
        self.reconstruction_loss_tracker.update_state(reconstruction_loss)
        self.kl_loss_tracker.update_state(kl_loss)
        return {
            "loss": self.total_loss_tracker.result(),
            "reconstruction_loss": self.reconstruction_loss_tracker.result(),
            "kl_loss": self.kl_loss_tracker.result(),
        }

# ---------- 训练模型 ----------
(x_train, _), (x_test, _) = keras.datasets.mnist.load_data()
mnist_digits = np.concatenate([x_train, x_test], axis=0)
mnist_digits = np.expand_dims(mnist_digits, -1).astype("float32") / 255

vae = VAE(encoder, decoder)
vae.compile(optimizer=keras.optimizers.Adam())
vae.fit(mnist_digits, epochs=10, batch_size=128)

VAE（变分自编码器）的概率论原理

通过前面的基本架构和代码示例，我们已经知道 VAE 是什么样子了。但是，为什么这个设计是有效的？

VAE 建立在坚实的概率论基础之上，其核心思想巧妙融合了生成模型与潜在变量模型的优势。

VAE 属于变分推断中的一种较好的实现方式。

用概率表示

一般的 Auto Encoder 中，输入 $x$ 会映射成隐空间中的一个固定长度的向量。在 VAE 中，输入映射成一个概率分布。用 $p_\theta$ 表示该分布，其中参数是 $\theta$ 。这样，输入 $\mathbf{x}$ 和隐空间的向量 $\mathbf{z}$ 可以如下定义：

先验： $p_\theta(\mathbf{z})$
条件分布 $p_\theta(\mathbf{x}\vert\mathbf{z})$
后验分布 $p_\theta(\mathbf{z}\vert\mathbf{x})$

假定我们知道这个分布的真实参数为 $\theta^{*}$ 。为了生成一个类似真实数据的点 $\mathbf{x}^{(i)}$ ，可以如下操作：

首先，从先验分布 $p_{\theta^*}(\mathbf{z})$ 中抽样一个值 $\mathbf{z}^{(i)}$
根据条件分布 $p_{\theta^*}(\mathbf{x} \vert \mathbf{z} = \mathbf{z}^{(i)})$ 生成数值 $\mathbf{x}^{(i)}$
最优参数 $\theta^{*}$ 是众多可能参数中，使生成的数据集（多个 $\mathbf{x}^{(i)}$ ）为真实概率最大的那个参数。

\theta^{*} = \arg\max_\theta \prod_{i=1}^n p_\theta(\mathbf{x}^{(i)}) \tag{3.1}

为了方便计算，一般将上式的右边部分，通过 log 将乘法变成加法。

\theta^{*} = \arg\max_\theta \sum_{i=1}^n \log p_\theta(\mathbf{x}^{(i)}) \tag{3.2}

引入隐变量后，上述过程可以表示为：

p_\theta(\mathbf{x}^{(i)}) = \int p_\theta(\mathbf{x}^{(i)}\vert\mathbf{z}) p_\theta(\mathbf{z}) d\mathbf{z} \tag{3.3}

似然难以求解（Intractability of the Likelihood）

在实践中，由于对边缘分布进行积分计算的成本非常高昂，需要遍历所有可能的 $\mathbf{z}$ ，故根据上面的公式 3.3， $p_{\theta}(\mathbf{x})$ 不好求解。通常想到的解决方案是使用后验分布，用贝叶斯法则来表示：

p_\theta(\mathbf{z} | \mathbf{x}) = \frac{p_{\boldsymbol{\theta}}(\mathbf{x}, \mathbf{z})}{p_{\boldsymbol{\theta}}(\mathbf{x})} \tag{3.4}

然而，从公式（3.4）可以看出， $p_{\boldsymbol{\theta}}(\mathbf{z} \vert \mathbf{x})$ 依赖于 $p_{\theta}(\mathbf{x})$ ，也不方便求解。

变分推断（Variational Inference, VI），Approximate Posterior（近似后验）

下面介绍变分推断对这个问题的解决思路。

为了加速对潜变量的搜索，我们希望通过引入一个近似函数来缩小潜变量的取值范围。这个函数表示为 $q_\phi(\mathbf{z} \vert \mathbf{x})$ ，它根据输入数据 $\mathbf{x}$ 输出潜变量 $\mathbf{z}$ 的可能分布。

$q_\phi(\mathbf{z} \vert \mathbf{x})$ 通常被称为推断模型（inference model）或变分后验（variational posterior）。它由参数 $\phi$ 表示， $\phi$ 是需要学习的参数（例如神经网络中的权重）。使用 $q_\phi(\mathbf{z} \vert \mathbf{x})$ 的目的是为了近似（approximate）生成模型的真实但难以计算的后验分布 $p_\theta(\mathbf{z} \vert \mathbf{x})$ ，从而简化优化过程（optimization）并提升计算效率。

q_\phi(\mathbf{z}|\mathbf{x})\approx p_{\boldsymbol{\theta}}(\mathbf{z}|\mathbf{x}) \tag{3.5}

$q_\phi(\cdot {\mid} \mathbf{x})$ 是从变分族 $\mathcal{Q}$ 中选择。高斯族（Gaussian family）是一个常见的选择，尽管也可以使用其他族（如分类族、泊松族等）。高斯族中一个常见的选择是同方差高斯分布（isotropic Gaussian）（对角协方差矩阵）。

q_\phi(\mathbf{z} | \mathbf{x}) := \mathcal{N}( \mathbf{z}\ |\ \mu_\phi(\mathbf{x}) , \sigma_\phi(\mathbf{x}) I ) \tag{3.6}

实现上，可以用神经网络实现该概率分布，输入为 $x$ ，输出 $\mu_\phi(\mathbf{x})$ 和 $\sigma_\phi(\mathbf{x})$ ：

(\boldsymbol{\mu},\log\boldsymbol{\sigma}) =\text{EncoderNeural}\mathrm{Net}_{\boldsymbol{\phi}}(\mathbf{x}) \tag{3.7}

由于这个推断模型（神经网络）的参数（ $\phi$ ）在数据集中的所有数据点中 $\{\mathbf{x}^{(i)}, \mathbf{y}^{(i)}\}_{i=1, \dots, N}$ 共享（分摊），故称为摊销变分推断（amortized variational inference），这样大幅提升了训练速度。非摊销变分推断则对每一个数据点 $\mathbf{x}^{(i)}$ 建立一个模型。

引入近似后验分布，使得可以将似然 $p_\theta (\mathbf{x})$ 表示为关于 $q_\phi(\mathbf{z} \vert \mathbf{x})$ 期望。

p_\theta (\mathbf{x}) = \int_\mathbf{z} p_\theta(\mathbf{x} ,\mathbf{z}) d \mathbf{z} = \int_\mathbf{z} \frac{q_\phi(\mathbf{z} | \mathbf{x})}{q_\phi(\mathbf{z} | \mathbf{x})} p_\theta(\mathbf{x}, \mathbf{z}) d \mathbf{z} = \mathbb{E}_{q_\phi(\mathbf{z} | \mathbf{x})} \left[ \frac{p_\theta(\mathbf{x}, \mathbf{z})}{q_\phi(\mathbf{z} | \mathbf{x})} \right] \tag{3.8}

对照（3.3）和（3.8），将积分问题变成了期望计算问题，通常来说，期望有数学公式或者更容易近似，后验近似 $q_\phi(\mathbf{z} \vert \mathbf{x})$ 的作用在此体现。

VAE 的学习过程

如下，从架构角度展示了 VAE 的基本思路。

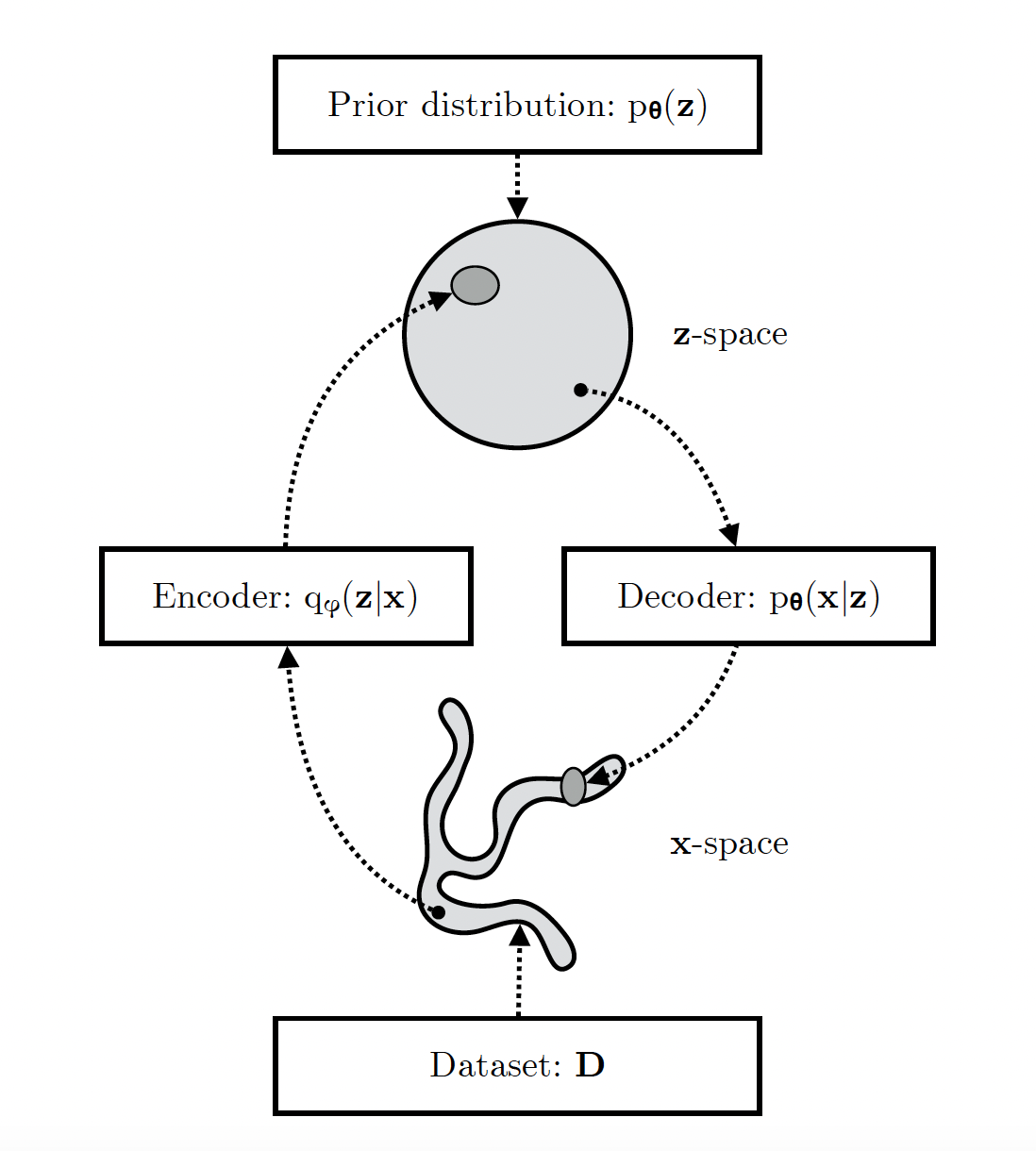图 10：VAE 的学习过程，图片来源：论文 1906.02691

VAE 学习过程中的几个要点：

VAE 学习了一个从观测空间 $x$ （x-space）到潜在空间 $z$ （z-space）的随机映射。
观测空间 x-space 的经验分布 $q_D(x)$ 通常较为复杂，而潜在空间 z-space 的分布可以相对简单（例如如图中所示的球形分布）。
生成模型 Decoder 学习一个联合分布 $p_{\theta}(x, z)$ ，该分布通常被分解为 $p_{\theta}(x, z) = p_{\theta}(z)p_{\theta}(x{\mid}z)$ ，其中 $p_{\theta}(z)$ 是潜在空间的先验分布， $p_{\theta}(x{\mid}z)$ 是一个随机解码器。
随机编码器 Encoder $q_{\phi}(z{\mid}x)$ （也称为推断模型）近似生成模型的真实但不可直接计算的后验分布 $p_{\theta}(z{\mid}x)$ 。

变分推断的几个步骤：

在变分推断中，我们通常需要构建一个对数似然函数的下界，这样可以简化优化问题，使得计算更加可行。
评估这个下界的紧密性是重要的，因为它决定了我们通过优化这个下界来近似真实对数似然的准确性。
摊销变分推断是一种变分推断的改进方法，它通过学习一个通用的推断模型来减少计算成本，而不是为每个数据点单独训练模型。
如何优化这个下界，通常涉及到选择合适的变分分布和优化算法，以提高推断的准确性和效率。

目标函数

对于（3.8）的计算，假如用 Monte-Carlo 方法估计 $\frac{p_\theta(\mathbf{x}, \mathbf{z})}{q_\phi(\mathbf{z} \vert \mathbf{x})}$ 的均值 $\mathbb{E}_{q_\phi(\mathbf{z} \vert \mathbf{x})} \left[ \cdot \right]$ 很不稳定，原因是 $\frac{1}{q_\phi(\mathbf{z} \vert \mathbf{x})}$ 不稳定。

既然完整计算不可行，是否可以找一个下界来逼近呢？这个下界越接近真实值越好。后面可以看出，证据下界（Evidence Lower Bound，简称 ELBO，也叫变分下界 variational lower bound）就是这个好的替代品。

证据下界（Evidence Lower Bound，ELBO）

有两种方法推导 ELBO，第一种是用詹森不等式（Jensen’s inequality），对（3.8）两边取对数，具体推导过程见（3.9）。

\log p_\theta (\mathbf{x}) = \log \mathbb{E}_{q_\phi(\mathbf{z} | \mathbf{x})} \left[ \frac{p_\theta(\mathbf{x}, \mathbf{z})}{q_\phi(\mathbf{z} | \mathbf{x})} \right] \geq \mathbb{E}_{q_\phi(\mathbf{z} | \mathbf{x})} \left[ \log \frac{p_\theta(\mathbf{x}, \mathbf{z})}{q_\phi(\mathbf{z} | \mathbf{x})} \right] =: \mathcal{L} (\mathbf{x}) \tag{3.9}

论文作者使用另一种推导方法（来源：论文 1906.02691），可以更方便看出 ELBO 作为下界的有效性。

\begin{align} \log p_\theta(\mathbf{x}) &= \mathbb{E}_{q_\phi(\mathbf{z}|\mathbf{x})} \left[ \log p_\theta(\mathbf{x}) \right] \tag{3.10.1} \\[1em] &= \mathbb{E}_{q_\phi(\mathbf{z}|\mathbf{x})} \left[ \log \frac{p_\theta(\mathbf{x}, \mathbf{z})}{p_\theta(\mathbf{z}|\mathbf{x})} \right] \tag{3.10.2} \\[1em] &= \mathbb{E}_{q_\phi(\mathbf{z}|\mathbf{x})} \left[ \log \left[ \frac{p_\theta(\mathbf{x}, \mathbf{z})}{q_\phi(\mathbf{z}|\mathbf{x})} \frac{q_\phi(\mathbf{z}|\mathbf{x})}{p_\theta(\mathbf{z}|\mathbf{x})} \right] \right] \tag{3.10.3} \\[1em] &= \underbrace{\mathbb{E}_{q_\phi(\mathbf{z}|\mathbf{x})} \left[ \log \frac{p_\theta(\mathbf{x}, \mathbf{z})}{q_\phi(\mathbf{z}|\mathbf{x})} \right]}_{\mathcal{L}_{\theta, \phi}(\mathbf{x}) \, \text{(ELBO)}} + \underbrace{\mathbb{E}_{q_\phi(\mathbf{z}|\mathbf{x})} \left[ \log \frac{q_\phi(\mathbf{z}|\mathbf{x})}{p_\theta(\mathbf{z}|\mathbf{x})} \right]}_{D_{\text{KL}}(q_\phi(\mathbf{z}|\mathbf{x}) \| p_\theta(\mathbf{z}|\mathbf{x}))}. \tag{3.10.4} \end{align}

等式（3.10.4）中的第一项即 ELBO，运用对数性质得到：

\mathcal{L}_{\theta,\phi}(\mathbf{x})=\mathbb{E}_{q_{\boldsymbol{\phi}}(\mathbf{z}|\mathbf{x})}\left[\log p_{\theta}(\mathbf{x},\mathbf{z})-\log q_{\phi}(\mathbf{z}|\mathbf{x})\right]

ELBO 有效性的解释

从上面公式（3.10.4）移项得：

\begin{aligned} \mathcal{L}_{\theta,\phi}(\mathbf{x})& =\log p_{\theta}(\mathbf{x})-D_{KL}(q_{\phi}(\mathbf{z}|\mathbf{x})||p_{\theta}(\mathbf{z}|\mathbf{x})) \tag{3.11}\\ &\leq\log p_{\theta}(\mathbf{x}) \end{aligned}

这样 ELBO 可以看成两部分的差：

既定事实 $\log p_{\theta}(x)$ ，这个可以看成常量。
$q_{\phi}(\mathbf{z}{\mid}\mathbf{x})$ 和 $p_{\theta}(\mathbf{z}{\mid}\mathbf{x})$ 两个概率分布的 KL 散度（第 1 个 KL 散度）。

由于 $p_{\theta}(x)$ 是固定值，因此，最大化 ELBO 即 $\mathcal{L}_{\theta,\phi}(\mathbf{x})$ 会同时优化两个点：

它将近似地最大化边际似然 $\log p_{\boldsymbol{\theta}}(\mathbf{x})$ ，这样生成模型将变得更好。
它将最小化 $q_{\phi}(\mathbf{z}|\mathbf{x})$ 与真实后验 $p_{\boldsymbol{\theta}}(\mathbf{z}|\mathbf{x})$ 之间的 KL 散度，从而使 $q_{\phi}(\mathbf{z}|\mathbf{x})$ 变得更好，从图 8 可以清晰看到这一点。

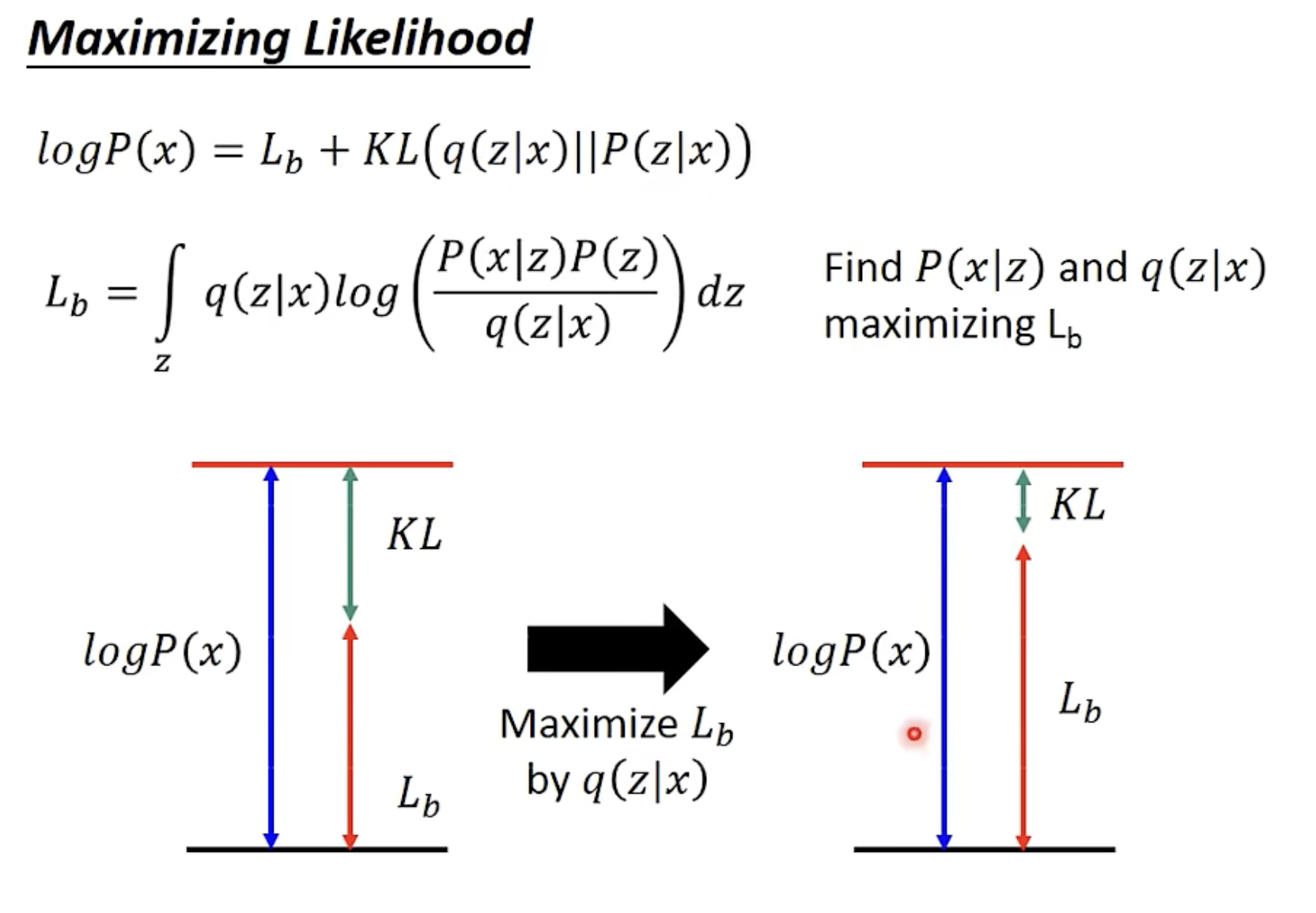图 8：为什么最大化 $L_b$ 有效？来源于李宏毅的人工智能课程 ppt

ELBO 的计算

有了目标函数，下面看如何有效计算 ELBO。

首先看 ELBO 的两种表示方式：

除了上面（3.10.4）的表示方法（记作方法 1）：

\mathcal{L}_{\theta, \phi} = \mathbb{E}_{q_\phi(\mathbf{z}|\mathbf{x})} \left[ \log \frac{p_\theta(\mathbf{x}, \mathbf{z})}{q_\phi(\mathbf{z}|\mathbf{x})} \right] \tag{3.12}

运用对数性质推演后，得到表示方法 2 更方便计算，见（3.13）：

\mathcal{L}_{\theta, \phi}(\mathbf{x}) := \mathbb{E}_{q_\phi(\mathbf{z} | \mathbf{x})} \left[ \log p_\theta(\mathbf{x} | \mathbf{z}) - \log q_\phi(\mathbf{z} | \mathbf{x}) + \log p_\theta(\mathbf{z}) \right] = \overbrace{ \mathbb{E}_{q_\phi(\mathbf{z} | \mathbf{x})} \left[ \log p_\theta(\mathbf{x} | \mathbf{z})\right] }^{\text{(a) Negative Reconstruction Error}} - \overbrace{ \mathcal{D}_{\operatorname{KL}}\left(q_\phi(\mathbf{z}|\mathbf{x})\ \Vert p(\mathbf{z})\right) }^{\text{(b) Regularization}} \tag{3.13}

从表示方法 2 （3.13）可以看出，ELBO 可以分为两个主要部分：重构损失（取反）（Negative Reconstruction Error）和正则化损失（Regularization）（第 2 个 KL 散度 ，后续章节记为 kl_loss）

注意：个别地方将这里表述为“重构损失”不太恰当，公式（3.13）中的含义是似然，是衡量重构 $x$ 的成功率，在计算损失函数时会取反。

优化 ELBO 会在项（a）和项（b）之间产生权衡。项（a）衡量重建质量，而项（b）则强制后验分布与先验分布（ $p(z)$ ，通常假定为标准正态分布）相匹配。正则化越强（即对KL散度项b的惩罚越大），获得良好重建的难度就越大。

了解了 ELBO 的分解，那如何分别求解呢？

重构损失（取反）（Negative Reconstruction Error）

重构损失衡量 VAE 的解码器 $p_\theta(\mathbf{x}{\mid}\mathbf{z})$ 从潜在变量 $\mathbf{z}$ 还原原始数据 $\mathbf{x}$ 的质量。

这样重构损失和 Auto-Encoder 的思路一致了，通过隐变量后，输出和输入尽量一致。参考下图。

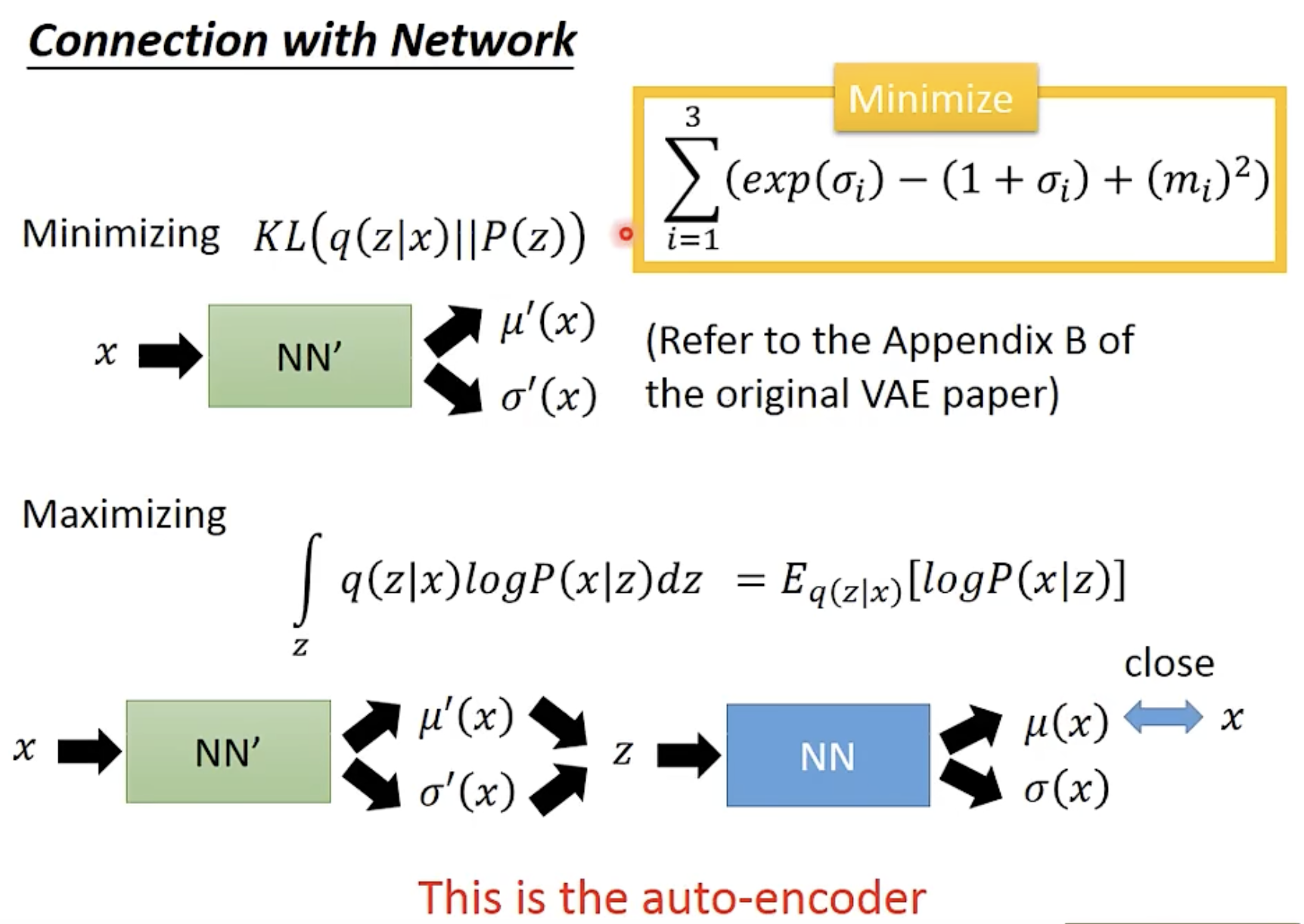图 9：如何最大化 $L_b$ 的第一部分？来源于李宏毅的人工智能课程 ppt

正则化损失

正则化损失是一个 Kullback-Leibler（KL）散度项，用于衡量编码器生成的近似后验 $q_\phi(\mathbf{z}{\mid}\mathbf{x})$ 与先验分布 $p_\theta(\mathbf{z})$ 的差异。

这一部分对潜在空间进行正则化，确保学习到的后验分布 $q_\phi(\mathbf{z}{\mid}\mathbf{x})$ 与先验分布 $p_\theta(\mathbf{z})$ 对齐。在大多数 VAE 中，先验分布 $p_\theta(\mathbf{z})$ 通常被设为简单的高斯分布 $\mathcal{N}(\mathbf{0}, \mathbf{I})$ 。因此，KL 散度鼓励潜在变量 $\mathbf{z}$ 的结构与这一高斯先验对齐。

直观理解，正则化损失通过鼓励潜在空间遵循平滑、有规律的分布（如高斯分布）来防止过拟合。此外，它确保解码器可以从先验分布中采样到有意义的潜在变量，并生成合理的输出。

正则化损失（ $-D_{KL}(q_{\phi}(\mathbf{z}{\mid}{x}){\Vert}p_{\theta}(\mathbf{z}))$ ），可以直接用统计分析的方法计算得到。下面是先验 $p(z) = \mathcal{N}({0},\mathbf{I})$ 和后验近似 $q_{\phi}(\mathbf{z}{\mid}\mathbf{x}^{(i)})$ 均为高斯分布时的求解方法。

设 $z$ 的维度为 $J$ 。设 $μ$ 和 $σ$ 分别为数据点 $i$ 变分后的均值和标准差，而 $μ_j$ 和 $σ_j$ 则简单表示这些向量的第 $j$ 个元素。那么：

\begin{aligned} \int q_{\phi}(\mathbf{z})\log p_{\theta}(\mathbf{z}) d\mathbf{z}& =\int\mathcal{N}(\mathbf{z};{\mu},{\sigma}^2)\log\mathcal{N}(\mathbf{z};{0},\mathbf{I}) d\mathbf{z} \\ &=-\frac J2\log(2\pi)-\frac12\sum_{j=1}^J(\mu_j^2+\sigma_j^2) \end{aligned}

同时：

\begin{aligned} \int q_{\boldsymbol{\phi}}(\mathbf{z})\operatorname{log}q_{\boldsymbol{\phi}}(\mathbf{z}) d\mathbf{z} & =\int\mathcal{N}(\mathbf{z};\boldsymbol{\mu},\boldsymbol{\sigma}^2)\log\mathcal{N}(\mathbf{z};\boldsymbol{\mu},\boldsymbol{\sigma}^2) d\mathbf{z} \\ &=-\frac J2\log(2\pi)-\frac12\sum_{j=1}^J(1+\log\sigma_j^2) \end{aligned}

综合上面两个公式，可以推导出计算 KL 损失的公式（请和代码对照看）。

\begin{aligned} -D_{KL}((q_{\phi}(\mathbf{z})||p_{\theta}(\mathbf{z}))& =\int q_{\phi}(\mathbf{z})\left(\log p_{\boldsymbol{\theta}}(\mathbf{z})-\log q_{\boldsymbol{\theta}}(\mathbf{z})\right) d\mathbf{z} \\ &=\frac12\sum_{j=1}^J\left(1+\log((\sigma_j)^2)-(\mu_j)^2-(\sigma_j)^2\right) \hspace{2em} (6.1) \end{aligned}

如上公式，请对照上面的 Python 训练代码，这里再列一下。

    kl_loss = -0.5 * (1 + z_log_var - tf.square(z_mean) - tf.exp(z_log_var))
    kl_loss = tf.reduce_mean(tf.reduce_sum(kl_loss, axis=1))

VAE 中的概率模型选择

先验分布 Prior $p_{\theta}(\mathbf{z})$

默认情况下，先验分布通常选择为简单的高斯分布（正态分布）：

p(\mathbf{z}) := \mathcal{N}(0, I)

后验分布 Posterior $q_\phi(\mathbf{z}|\mathbf{x})$

后验分布被选择为与先验分布属于相同的变分族。当使用重参数化技巧时，后验分布必须允许重参数化。一个与高斯先验相匹配的常见选择是对角高斯分布：

q_\phi(\mathbf{z} | \mathbf{x}) := \mathcal{N}( \mathbf{z}\ |\ \mu_\phi(\mathbf{x}) , \sigma_\phi(\mathbf{x}) I )

对角高斯分布（Diagonal Gaussian Distribution）是指其协方差矩阵为对角矩阵的高斯分布。这意味着在这个分布中，各个维度（或变量）是独立的，并且每个维度都有自己的均值和方差（或标准差）。

观测模型 Observation Model $p_\theta(\mathbf{x} \vert \mathbf{z})$

观测模型的选择取决于特征的性质，因此，对于二值像素值，一个合适的重构分布选择是伯努利分布。

p_\theta(\mathbf{x}|\mathbf{z}) = \prod_i \mathcal{B}(x_i | g_\theta(\mathbf{z})) = \prod_i g_\theta(\mathbf{z})_i^{x_i} \cdot (1-g_\theta(\mathbf{z})_i)^{1-x_i}

上式中， $x_1, \dots, x_D \in \{0,1\}^{D}$ 代表图像的像素值 $\mathbf{x}$ ，假如图像有 784 个像素，则 $D$ 为 784。 $x_i$ 的取值为 0 (黑) 或者 1（白）。

$g_\theta$ 是 VAE 的解码器。 $g_\theta(z)_i$ 表示生成第 $i$ 个像素值为 1（白）的概率。

之所以可以这样做，是因为我们假设像素强度是 i.i.d.（独立且同分布）的，即 $p(\mathbf{x}) = \prod_i p(x_i)$ ，因此不需要直接对它们之间的相关性建模。尽管如此，我们仍然通过潜在变量 $\mathbf{z}$ 实现了间接的条件相关性。

这个思路下设计的损失函数，对应上面的代码

        reconstruction_loss = tf.reduce_mean(
            tf.reduce_sum(
                keras.losses.binary_crossentropy(data, reconstruction),
                axis=(1, 2),
            )
        )

如何理解重构损失的计算

Q：和原始值做对比的原理是什么？（重构损失）
Decoder 神经网络输出的 $x$ 的预测值，而 ELBO 计算的是生成正确的 x 概率（ $p(x\vert z)$ ），故需要和原始值做对比判断重构损失。
以上面的二值像素值为例，如果共 5 个像素，真实像素为[1, 0, 1, 1, 0]，Decoder 网络输出为[0.8, 0.3, 0.7, 0.9, 0.1]，成功生成原图的 log 概率（似然）可以用二分类交叉熵计算，损失函数 keras.losses.binary_crossentropy 会取反。具体可参考交叉熵损失函数（Cross Entropy Loss）：图示+公式+代码。

应用

视频生成 Sora 使用了 VAE 方法。

以下内容摘自Video generation models as world simulators

We train a network that reduces the dimensionality of visual data.[20] This network takes raw video as input and outputs a latent representation that is compressed both temporally and spatially. Sora is trained on and subsequently generates videos within this compressed latent space. We also train a corresponding decoder model that maps generated latents back to pixel space.
[20] Kingma, Diederik P., and Max Welling. “Auto-encoding variational bayes.” arXiv preprint arXiv:1312.6114 (2013).